Your cart is empty
Theoretical Underpinnings of the Programme
- NumberSense specific research (Brombacher, Roberts)
Chapter 14:
The NumberSense programme: A focus of the Shikaya intervention in South Africa
We know that difficulties with learning mathematics stem from early on in the primary school. What to do – at scale – to ensure that children exiting Foundation Phase are ready to thrive mathematically is less well known. This research reports on interventions that show promise in early grade mathematics, noting both their impact as well as the characteristic design features, which are thought to be driving that change. Design-based approaches to creating well designed and structured learning and teaching materials, which then clearly articulate the necessary conditions for uptake and fidelity of implementation, are therefore helpful. Drawing first on secondary sources we demonstrate promising impacts of the NumberSense Programme in South Africa and Jordan. We then focus explicitly on the Shikaya intervention, exploring five years of Early Grade Mathematics Assessment (EGMA) data (n = 11,516) to report on shifts in attainment with each cohort. The preliminary analysis over the first three years was promising, but was then interrupted by the Covid pandemic. The design features of the NumberSense workbooks are described. The impact of the Shikaya intervention model ought to be more rigorously evaluated, to establish the extent to which it holds promise for learning improvements at scale.
Brombacher, A., Roberts, N. (2022). The NumberSense programme: A focus of the Shikaya intervention in South Africa. In Early Grade Reading and Mathematics Interventions in South Africa (pp. 265–280).
The full publications:
Early Grade Interventions in South Africa: Reading and Mathematics
Three volumes of current research, complied by Oxford University Press, which focuses on developments in early grade reading and mathematics in South Africa between 2010 and 2022: ‘Edited by Nic Spaull and Elizabeth Pretorius, Hamsa Venkat and Nicky Roberts, and Nic Spaull and Stephen Taylor respectively, the three books collectively bring together 77 authors from diverse disciplines, most of whom are South African researchers well known in the field of early grade reading and mathematics. The volumes seek out insights from lessons learned in the last decade, including whether reading and mathematics outcomes have improved, why they have improved, and why the post-improvement level of performance is still so low, concluding with an analysis of what interventions work and what scales. The collection will interest local and international researchers, as well as policy-makers and donors, who want to know not only what works, but also why it works, how it works, and where it works.’ (Oxford University Press)
The ePDFs are available for download on the Oxford University Press SA Resource hub website.
NumberSense Research (Chapter 14) - Mathematics as a sense-making, problem-solving activity (Mathematical Proficiency: Kilpatrick, Swafford, Findell)
A teacher’s understanding of what it means to do mathematics profoundly influences how she will teach mathematics. If a teacher’s understanding of doing mathematics involves memorising facts, rules, formulae and procedures to determine the answers to questions then she will teach in a particular way. By contrast, if a teacher regards doing mathematics as a sense-making, problem-solving activity, then her teaching approach will be quite different.
In our view, doing mathematics is much more than “getting lots of answers right”. In the book Adding It Up (Kilpatrick, Swafford & Findell, 2001), the authors describe doing mathematics as being mathematically proficient. The authors introduce mathematical proficiency as follows:
“Our analyses of the mathematics to be learned, our reading of the research in cognitive psychology and mathematics education, our experience as learners and teachers of mathematics, and our judgment as to the mathematical knowledge, understanding, and skill people need today have led us to adopt a composite, comprehensive view of successful mathematics learning. Recognizing that no term captures completely all aspects of expertise, competence, knowledge, and facility in mathematics, we have chosen mathematical proficiency to capture what we think it means for anyone to learn mathematics successfully.”
(Adding it Up, Kilpatrick, Swafford & Findell, 2001, page 5)
The authors go on to describe mathematical proficiency (i.e. being able to do mathematics) as having five interrelated dimensions or strands.
The strands of mathematical proficiency are:
- Conceptual understanding (understanding): comprehension of mathematical concepts, operations, and relations.
- Procedural fluency (computing or calculating): skill in carrying out procedures flexibly, accurately, efficiently, and appropriately.
- Strategic competence (applying): ability to formulate, represent, and solve mathematical problems.
- Adaptive reasoning (reasoning): capacity for logical thought, reflection, explanation and justification.
- Productive disposition (engaging): habitual inclination to see mathematics as sensible, useful and worthwhile, coupled with a belief in diligence and one’s own efficacy.
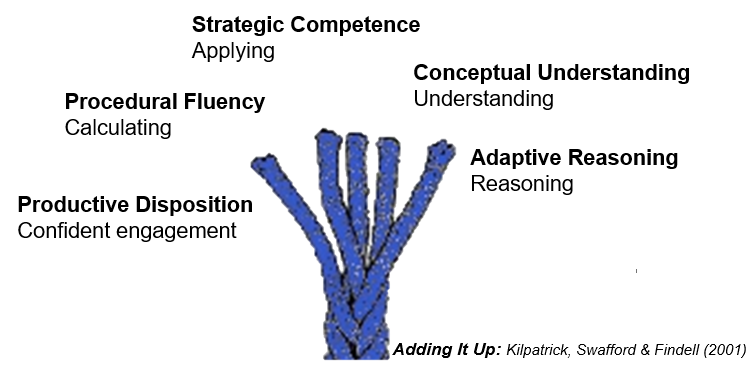
The five strands are interwoven and interdependent. We want children to develop a wide range of calculation strategies (procedures) that they can apply with confidence and understanding, able to reason about what they have done. Finally, we also want children to develop a disposition towards doing mathematics in which they recognise that they need to engage in doing mathematics in order to learn mathematics.
Mathematical proficiency and the NumberSense Mathematics Programme
In the NumberSense Mathematics Programme this view of what it means to do mathematics is translated into the activities in a range of ways:
- In the workbooks, we do not prescribe calculation strategies but rather introduce children to a range of different strategies with the expectation that they will develop the ability to apply these strategies fluently (with confidence) and flexibly (selecting calculation strategies or problem-solving approaches that are appropriate to the situation at hand).
- Children are presented with unfamiliar situations in which they are expected to apply what they already know to makes sense of the situation and solve the problem.
- Children are frequently asked either explicitly (for example, “What did you notice?”) or implicitly (for example, in extending patterns) to reflect on what they have done, forcing them to reason and develop their understanding of what they are doing. The role of the teacher in this regard cannot be overstressed: the expectation is that teachers will, instead of checking answers only, review activities by asking questions such as: “What did you notice?”; “How did you do that?”; “How was this activity similar to or different from previous activities?” etc.
- There is a lot of repetition. Children revisit the same concepts again and again, although in increasing number ranges and in different representations. This is done firstly to provide practice and secondly to allow children to increase their confidence.
In developing the NumberSense Mathematics Programme, we have adopted a complex understanding of what it means to do mathematics – an understanding that doing mathematics means much more than the production of correct answers. We regard mathematics as a sense-making, problem-solving activity.
Adding it Up - How children learn mathematics (The Different Knowledge Types: Piaget)
Piaget distinguished between three different types of knowledge – physical knowledge, social knowledge and conceptual (logico-mathematical) knowledge. When thinking about how children learn mathematics, it is important to be mindful of these different knowledge types and how they are related.
Before discussing how the NumberSense Mathematics Programme takes account of these different knowledge types, each one is described in some detail.
Physical Knowledge:
This is the kind of knowledge which children acquire through interaction with the physical world, for example through observing and handling objects. Physical knowledge is derived from concrete experiences: touching, using, playing with and acting on concrete material. Children need a lot of concrete experiences in the mathematics classroom to develop their physical knowledge of number by counting concrete apparatus. It is through counting physical objects that children develop a sense of the size of numbers: 50 takes longer and more actions to count than 5 does, but 250 takes a lot more. Five counters can be held in one hand, 50 in two hands, while 250 require a container as there are too many for our hands. Five counters look different from two counters etc.
Counting physical objects like counters is called rational counting: the counters are physically handled and moved from one place to another. The children observe the pile of counters grow as they count them. The implication of physical knowledge for the mathematics classroom is very simply that there must be both concrete apparatus (counters, measuring apparatus, shapes such as building blocks and other construction materials) and the opportunity for children to work/play with the apparatus. It is the teacher’s responsibility to provide the materials and the time for children to use them. Interestingly, when it comes to learning geometric thinking, “play” or “physical knowledge” is vital to the formation of geometric understanding at any age.
Social Knowledge:
The number five is an unproblematic concept for an adult who has known and used the word for many years. An adult can imagine five items and can even calculate with five without having to recreate the number using physical counters or representations in their minds. However, if we take a moment to reflect and think about this, then we realise that the word five has no intrinsic properties that hint at the number of items it represents. So it is with people’s names, place names, days of the week and months of the year. The words we use to describe these are all “names” that we have assigned; because the people in our community (society) all associate the same thing with the same name (word) we are able to communicate with each other. In order to know these names (social knowledge), we need to be told the names and to remember them.
We refer to knowledge that must be both told and remembered as social knowledge. Conventions are another example of social knowledge. In some countries people drive on the left side of the road while in others they drive on the right side of the road. There is no “correct” side of the road to drive on. However, if all of the people in a country don’t agree to drive on a particular side, then there would be chaos. A good example of a mathematical convention is the so-called “order of operations convention” that guides us in determining the value of the statement 5 + 2 × 3. It is possible to imagine at least two different values for the statement:
- 21 which is the result of first adding the 5 and the 2 and multiplying the answer by three (i.e. working from left to right).
- 11 which is the result of first calculating the value of 2 × 3 and then adding the 5.
As with the sides of the road example, there is no inherent reason for either solution being correct. However, because we want everybody who calculates the value of the statement 5 + 2 × 3 to get the same value, we have introduced a convention called “the order of operations convention”. The implication of social knowledge for the mathematics classroom is that there is certain knowledge that teachers have to tell (teach). That is, they have to introduce children to the vocabulary and conventions of mathematics. The way in which we write the number symbols is also a socially agreed on convention and it is the job of the teacher to introduce children to these conventions. The words “addition, subtraction, division and multiplication” and the symbols that we use to denote them are all also examples of social knowledge. The challenge for the mathematics classroom is to distinguish between knowledge that must be told (social knowledge) and knowledge that children can construct for themselves (see conceptual knowledge).
Conceptual (logico-mathematical) Knowledge:
When children reflect on activities and begin to see patterns, relationships, regularities and irregularities within and between the numbers and the operations, they are constructing what is known as logico-mathematical knowledge. Logico-mathematical knowledge is internal knowledge and is constructed by each individual for themselves.
The teacher’s role in the development of children’s logico-mathematical knowledge is two-fold. On the one hand the teacher is responsible for creating activities and situations (problems) that will reveal the underlying structures of numbers, operations, and relationships. On the other hand, the teacher needs to actively encourage children to reflect on what they are doing and what they are thinking. The teacher should be helping them to express these ideas in words so that they can explain their actions to others, discuss their respective methods and even argue about the validity of each.
Since the teacher is unable to teach logico-mathematical knowledge through direct instruction, one of the most important tasks of teaching is to design situations from which children can develop their logico-mathematical knowledge. When designing a task, the teacher needs to ask, “What do I want children to learn from this situation/problem/activity?” Having established what the teacher wants children to learn, she then needs to shape the situation/problem/activity in a way that will provoke children to “see” the patterns and structures. Then, both during and on completion of the activity, the teacher needs to facilitate reflection on the activity by the child. This reflection, more than anything else, will provoke the development of logico-mathematical knowledge.
Knowledge types and the NumberSense Mathematics Programme
In the NumberSense Mathematics Programme, we are mindful of the different knowledge types and the relationship between them:
- Physical knowledge: In the early workbooks there are a lot of counting activities involving physical objects. The physical counting activities are critical for children to develop a sense of the ‘muchness’ of number. When children physically draw solutions to problems (an early problem-solving strategy) they are using their physical understanding of the problem to solve the problem.
- Social knowledge: Throughout the workbooks, social knowledge, such as vocabulary and conventions, is introduced in a deliberate way, often with a text box.
- Conceptual (logico-mathematical) knowledge: The overriding approach adopted in the NumberSense Mathematics Programme is to present children with situations that they must engage with in order to understand. These situations are designed to reveal an underlying mathematical structure. Through the reflection questions in the workbooks and the teacher’s all-important role of facilitating reflection (see earlier discussion), children develop a deeper conceptual understanding of the mathematics they are learning.
- Learning through play (Developing Geometric Thinking: Van Hiele)
According to van Hiele (1986), there are five levels of geometric thought that are sequential and hierarchical. These include visualisation, description, abstraction, deduction and rigour (although it is unlikely that children in the early grades will move beyond the descriptive level).
For children to function at any given level, they must have developed confidence at the preceding level. Progression from one level to another is largely based on instruction and experience rather than age or physical development.
For a child at the visual level of geometric thinking, figures and shapes are identified in terms of what they ‘look like’. If asked why a square is a square, a child will say that it is a square because it looks like one. However, if the square is tilted so that its sides appear to be at a 45˚ angle, then the child may not recognise the shape as a square, instead, they may call it a diamond.
Children at the descriptive level of geometric thinking recognise the properties of shapes. Children at this developmental level may identify a shape as a square because the shape has four sides that are the same length, or because the angles are right angles. However, at this level, the properties are not yet logically ordered or related. Children at this developmental level may identify a shape as an equilateral triangle because the shape has three sides that are equal in length, or because the shape has three angles that are equal in size. However they don’t recognise a relationship between the properties and cannot yet see a relationship between the equal angles and the equal sides of the equilateral triangle.
Recognising the relationships between the different properties of shapes happens during the deductive level of geometric thinking. Children at this developmental level are able to deduce some unknown properties of a shape from the known properties of the shape.
Teachers of children in the early grades typically work with children who are at the visual level of geometric thinking. The teacher’s role is to create learning situations that develop the children’s confidence in moving from the visual to the descriptive level of geometric thinking. Such learning situations can even lead to the informal deductive level. Van Hiele described five kinds of activities that promote the transition from one level to the next. These activities are as follows:
- Free play (inquiry phase): Children are given materials that encourage them to explore and become aware of certain structures.
- Focused play (direct orientation): Tasks are presented in such a way that the characteristic structures of the objects gradually appear to children.
- Explicitation: The teacher introduces terminology.
- More focused play (free orientation): The teacher presents tasks that can be completed in different ways and supports children in developing an awareness of what they have already noticed.
- Integration (seldom included in geometric activities in the early years): Children are given opportunities to synthesize what they have learned (van Hiele, 1999).
Learning through play and the NumberSense Mathematics Programme
Developing geometric thinking in the early grades is reliant on play and playing with resources. The activities in the NumberSense Companion series are deliberately structured to move children through the levels of geometric thinking by paying attention to the activities described by van Hiele. The role of the teacher in developing children’s geometric thinking is to:
- Organise the learning situations (activities) described in Companion Workbooks and Teacher Guides so as to direct the children’s attention to the geometric properties of shapes and objects.
- Introduce terminology.
- Engage the children in reflective discussion on the activities, encouraging explanations that incorporate appropriate geometric terms.
Learning through Play (Pierre Van Hiele)
