Your cart is empty
Concept Development
- The Stages of Number Development
As children develop their sense of number there are clearly identifiable developmental stages:
- Counting all
- Counting on
- Breaking down and building up numbers
When we observe children at work with numbers, solving problems with numbers in particular, we can tell at what stage of number development they are at.
- If we ask a child to calculate 3 + 5 and we observe that she “makes the 3” and “makes the 5” (using fingers or objects) before she combines the objects and counts all of them to determine that 3 + 5 = 8, then we say that this child is at the counting all stage.
- If we observe the child becoming more efficient by “making” only one of the numbers (using fingers or objects) and then counting these objects on from the other number 5: 6, 7, 8… to conclude that: 5 + 3 = 8, then we say that this child is at the counting on stage.
- If we observe a child, manipulating numbers to make the calculation easier, for example by saying that 8 + 7 = 8 + 2 + 5 = 10 + 5 = 15, we say that she has reached the breaking down and building up stage. What the child has done is to break up one of the numbers: 7 into 2 and 5, which allows her to “complete the 10” by adding the 2 to the 8 and then adding the remaining 5 to the 10 to get 15. We formally refer to this stage as the decomposing, rearranging and recomposing stage.
It is expected that all children reach the breaking down and building up stage within age-appropriate number ranges. In the early grades, we support children’s development of number sense and progression through the stages of number development through three distinct but interrelated activities: counting, manipulating numbers and solving problems.
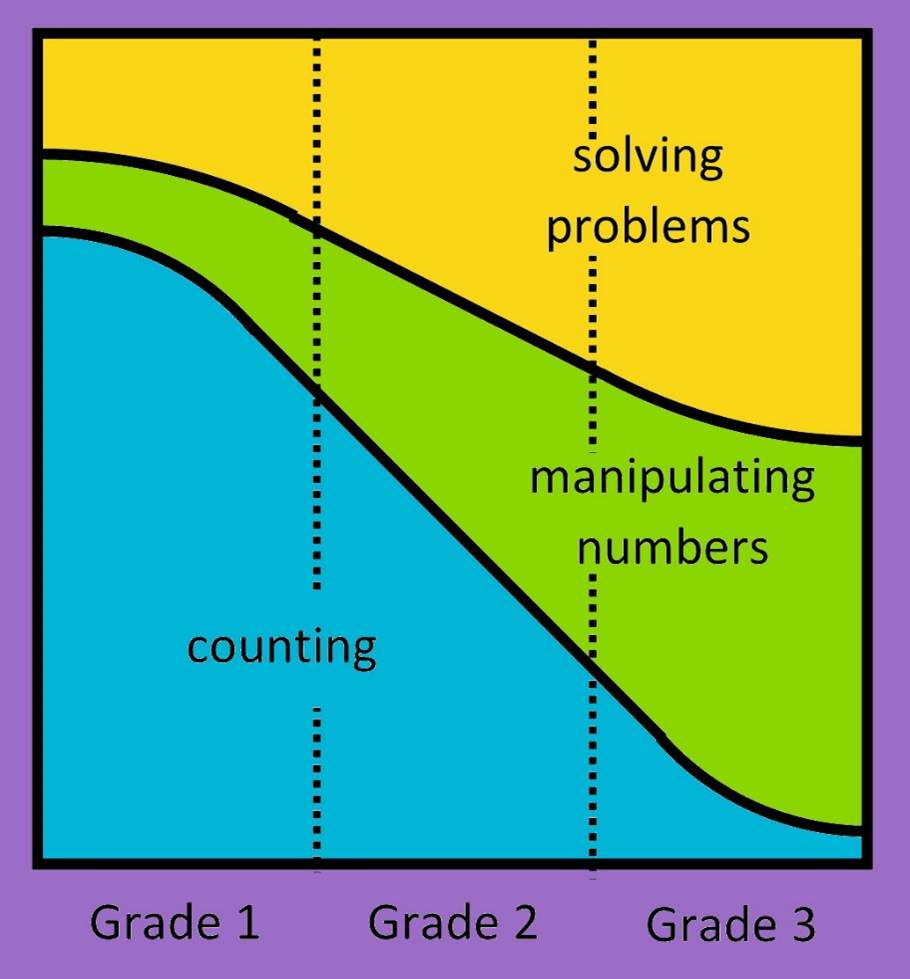
The amount of time that is spent on each of these activities will change over time as illustrated alongside.
Stages of number development and the NumberSense Mathematics Programme
In the NumberSense Mathematics Programme, we are mindful that children’s sense of number progresses through the three stages. The activities in the workbooks are sensitive to the stage at which the child is expected to be while simultaneously encouraging the child to move along the developmental trajectory. That said, by the time that children reach Workbook 6 we expect children to be breaking down and building up numbers within age-appropriate number ranges and by means of an increasingly larger range of strategies. These different strategies are more explicitly developed in Workbooks 13 to 24. Each page of the first twelve workbooks typically addresses the three key activities – counting, manipulating numbers and solving problems – in an integrated way. The amount of counting gradually decreases in Workbooks 9 through 14.
Counting, Manipulating Numbers and Problem Solving - Developing Number Sense: Counting
Why is Counting Important?
Humans have a natural curiosity and tendency to compare:- Who has the most? Who has the least?
- Who is tallest? Who is shortest?
- Who is heaviest? Who is lightest?
- Do I have enough? Do I have too much?
- Which route is the longest? Which route is the shortest?
In many situations, we can hold objects next to each other and make direct comparisons. However, when we cannot hold the things we are comparing next to each other, we need a “measuring device”. Measuring devices start out informally: fingers, hands, paces and so on. With time, these measuring devices become both more efficient and standardised. As much as we compare objects, we also need to compare the quantity of a collection of objects.
Counting plays three important roles in the lives of children:
- Counting develops the language of number.
- Giving meaning to the words often learnt through number songs and rhymes.
- Counting develops a sense of ‘muchness’ – quantity or numerosity:
- The idea that 5 is a small number, 50 a bigger number and 500 a much bigger number.
- The last number ‘counted’ tells us the size or measure of the group.
- Counting provides an early tool for calculating and solving problems.
Teacher Activities (detail in the handout)
Rote Counting
- Counting in 1s
- Number songs and rhymes
- Counting in steps
Rational Counting
- Using number cards
- Counting small piles of counters individually
- Counting out a given number
- Estimating and counting in 1s
- Counting in groups – body parts
- Counting large piles of counters
Written Activities in the NumberSense Workbooks
The NumberSense Workbooks contain various counting activities. This includes (but is not limited to):- Counting in 1s or groups
- Counting groups
- Counting mixed groups
- Number patterns
- Number lines
- Number worms
- Less and more activities
Counting Extract from: Counting, Manipulating Number and Problem SolvingCounting, Manipulating Numbers and Problem Solving - Developing Number Sense: Manipulating Numbers
Calculating Fluently and Efficiently
Numbers and calculations with numbers are at the heart of mathematics. Children need to develop a range of calculating strategies that enable them to calculate flexibly and fluently. Furthermore, it is important that they can perform a wide range of calculations mentally. Mental calculations are central to estimating. It is unlikely that we would expect anybody to spend time calculating 24.382 × 0.248 using paper and pencil in a context where we have calculators. However, it is important that a person has a sense of what the expected answer is. In the case of 24.382 × 0.248 we expect a person to have a sense that 24.382 × 0.248 ≈ 12 × 0,5 = 6 so that when they use their calculator and get 6.046736 as the answer they are not surprised.- Calculating flexibly means using different calculation strategies for different situations.
- Calculating fluently means confidently using a range of calculation strategies within a number range and for operations appropriate to a child’s developmental state.
Teacher Activities (detail in the handout)
- Single-digit arithmetic
- Multiples of 10, 100, 1000
- Completing 10s, 100s, 1000s
- Bridging 10s, 100s, 1000s
- Doubling and Halving
- Multiplication facts
Written Activities in the NumberSense Workbooks
The NumberSense Workbooks contain various manipulating numbers activities. This includes, but is not limited to:- Equivalent expressions (number sentences)
- Flow diagrams
- Number chains
- Tables
- Bubbles
- Number pyramids
- “Make less and more”
- “Guess my number”
Manipulating Numbers Extract from: Counting, Manipulating Numbers and Problem SolvingCounting, Manipulating Numbers and Problem SolvingManipulating Numbers videos for Workbooks 2-12Manipulating Numbers Resources - Developing Number Sense: Problem Solving
The Role of Problems
Mathematics is a tool for solving problems. Problems, however, also provide a way of supporting the learning of mathematics. Problems in the context of a problem-driven approach to learning serve three key purposes:
- They introduce children to the mathematics that we want them to learn.
- They help children to develop efficient computational strategies.
- They help children to experience mathematics as a meaningful, sense-making activity.
Children can add, subtract, multiply and divide long before they know these words. When a mother gives her children some sweets and asks them to share them equally between themselves they can do so.
Living organisms are natural problem solvers. Consider a plant growing in the ground. If the root meets a stone, it grows around the stone. When an animal senses danger, it will run away and hide or change colour or attack the perceived danger. When a young baby is hungry, they will cry to get attention. Children who come to school know how to solve problems, what they do not know are the labels that adults use to describe their natural responses to a problem. This is particularly true in mathematics.When we present a young child with some toy animals and a pile of counters and ask the child to share the counters equally between the animals they will do so. Try it! You will be amazed. Young children have naturally efficient strategies for sharing the counters between the toy animals. Young children can solve this problem and problems like it long before they can count the counters in the pile, long before they know what it is to divide and long before they can write a number sentence to summarise the problem situation and its solution.
In a problem-driven approach to learning mathematics, we present children with problem situations that they are capable of solving and where the natural solution strategy they use is the mathematics we want them to learn in a more formal way. In other words, we use a problem to provoke a natural response and that response is the mathematics we want to teach.
Teacher Activities (detail in the handout)
- Introducing mathematics
- Developing strategies
- Primitive drawings
- Sophisticated drawings
- Primitive number strategies
- Sophisticated number strategies – low
- Sophisticated number strategies – high
- Meaningful mathematics
- Classroom management
Written Activities in the NumberSense Workbooks
In the NumberSense Mathematics Programme, we use problem situations to introduce children to the different age-appropriate mathematical concepts. Typically we use problems to introduce children to:
- The basic operations and increasingly efficient number range-appropriate calculation strategies: Workbooks 1 to 12
- Fractions and operations with fractions: Workbooks 7 to 24
- Ratio, rate and proportion: Workbooks 15 to 24
- Patterns, algebra and problem-solving equations: Workbooks 13 to 24
Problem Solving Extract from: Counting, Manipulating Numbers and Problem SolvingCounting, Manipulating Numbers and Problem Solving - Developing the Fraction Concept
The handouts and resources below outline and illustrate the content from a NumberSense Mathematics Programme workshop which covered the following:
- Issues that underpin a deep and meaningful understanding of fractions.
- The developmentally-appropriate sequence for teaching fractions from Grade 2 to Grade 7 used in the NumberSense Workbooks.
- Assumptions and misconceptions about the teaching of fractions.
- The role of problems in learning about fractions and experiencing mathematics as a meaningful, sense-making activity.
Developing the Fraction Concept in the Foundation PhaseDeveloping the Fraction Concept in the Intermediate PhaseThe Development of the Fraction Concept Trajectory - Developing Pre-Algebraic Thinking
The handouts and resources below outline and illustrate the content from a NumberSense Mathematics Programme workshop which covered the following:
- The role of patterning in developing number sense in particular and mathematical proficiency in general.
- An appropriate trajectory of teaching and learning activities to support the development of patterning.
- Patterns, representations and interrelationships.
- Patterns and pre-algebra in the NumberSense classroom.
Developing the Function Concept (Patterns and Patterning) in the Primary SchoolThe Development of Algebraic Thinking Trajectory - Developing Geometric Thinking
The handouts and resources below outline and illustrate the content from a NumberSense Mathematics Programme workshop which covered the following:
- Developing geometric thinking in a NumberSense classroom with the focus on understanding, application and reasoning
- Van Hiele’s levels of geometric thinking and phases of learning.
- An exciting and innovative range of interactive and grade-appropriate NumberSense geometry activities.
Developing Geometric Thinking in the Primary SchoolLearning through Play (Pierre Van Hiele)
